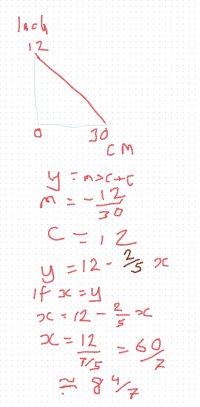Logic puzzle corner

[The Tall Luthier]

You have to drive 12km in your California.

You drive the first 6km at an average speed of 30km/h.

How fast do you need to drive the remaining 6 km to achieve an average speed of 60km/h for the whole journey?

First half is 12 minutes long
Total journey time allowed is 12 minutes

Part 2 : Really very quickly,

 

[California_Ocean]

First half is 12 minutes long
Total journey time allowed is 12 minutes

Part 2 : Really very quickly,

Exactly, it's impossible as currently a VW California can't exist in two places at the same time.

 

[The Tall Luthier]

Another one, not so famous.

You set out at 9am in your Cali to go to the top of the mountain col. Stop for coffee for 30mins at 11:15, then 45 minutes for lunch at 2pm you arrive at 6pm!

The following day you drive back down but leaving at 10am you stop for a pee at 12 for three minutes, lunch at 1:30 for fifteen minutes and back by 4pm (It's Downhill)

Is there any single point on the road that you passed at the same time of day on both journey days?

 

[Amarillo]

Another problem @Amarillo if you don’t mind.

Three garage doors, there’s a two tone Ocean behind one of them, the others are empty.

You have two chances to guess the right door.

After your first guess, say door one, the dealer will raise a different door that they know is an empty garage. One of doors two or three must be empty.

You then get to change your mind, if you want to. Should you?

The answer is yes you should, but why?

The answer is yes because the dealer is giving you additional information.

When you chose your door it had a 33% chance of being the correct door. By opening a door that the dealer KNOWS is empty, your door still has a 33% chance of being correct, but the other unopened door has a 67% chance of being correct.

The matter is different if the dealer doesn’t know if the door he opens has a California or not.

How is it different, and what should the customer do?

 

[GrahamB]

Exactly, it's impossible as currently a VW California can't exist in two places at the same time.

Unless it’s Schroedinger’s Cali?

 

[The Tall Luthier]

The answer is yes because the dealer is giving you The answer is yes because the dealer is giving you additional information.

When you chose your door it had a 33% chance of being the correct door. By opening a door that the dealer KNOWS is empty, your door still has a 33% chance of being correct, but the other unopened door has a 67% chance of being correct.

The matter is different if the dealer doesn’t know if the door he opens has a California or not.

How is it different, and what should the customer do?

agreed

It’s easier to contemplate if there were a thousand doors, you pick one and they choose 998 doors that are empty. Your instinct then tells you to swap.

Your first guess had a probability of 1/1000
The second guess, if you swap, is a one in two chance.

 

[Amarillo]

agreed

It’s easier to contemplate if there were a thousand doors, you pick one and they choose 998 doors that are empty. Your instinct then tells you to swap.

Your first guess had a probability of 1/1000
The second guess, if you swap, is a one in two chance.

Noel Edmond’s deal or no deal is a similar game.

I’m fairly confident that Edmond’s has no information that he impart either deliberately or sub-consciously. But what I don’t know is if the “banker” gives information in their offers or if offers are generated impartially, based only on what is known to the contestant.

 

[The Tall Luthier]

Noel Edmond’s deal or no deal is a similar game.

I’m fairly confident that Edmond’s has no information that he impart either deliberately or sub-consciously. But what I don’t know is if the “banker” gives information in their offers or if offers are generated impartially, based only on what is known to the contestant.

A very similar idea however mathematically much simpler. the chance of winning in DOND is always 1/n where n is the number of boxes. All other information is fluff.
In the Monty Hall problem the maths does involved Baye's Theorem of conditional probability which makes it a little more interesting.

Did you get any where with the Cali goes up a mountain problem? #28

 

[Amarillo]

Did you get any where with the Cali goes up a mountain problem? #28

I’ve just checked Wikipedia about DOND, and you are right: it is all fluff.

If we go back to the Monty Hall problem and shove £million behind one of the doors. After an empty door is revealed, the host could offer the contestant £500,000 to withdraw.

While there is a 67% chance of the contestant winning £1,000,000, valuing withdrawal at £666,666.67, there are legitimate reasons for the contestant to accept £500,000 to withdraw.

That is the drama of DOND.

I was out walking Meg when I read your problem and need a paper and pencil to properly consider it. I’ll do it, but possibly not until after the boys are in bed.

 

[Amarillo]

Another one, not so famous.

You set out at 9am in your Cali to go to the top of the mountain col. Stop for coffee for 30mins at 11:15, then 45 minutes for lunch at 2pm you arrive at 6pm!

The following day you drive back down but leaving at 10am you stop for a pee at 12 for three minutes, lunch at 1:30 for fifteen minutes and back by 4pm (It's Downhill)

Is there any single point on the road that you passed at the same time of day on both journey days?

Yes, sometime between 12.37 and 12.38, assuming constant speed on each day.

 

[Amarillo]

Yes, sometime between 12.37 and 12.38, assuming constant speed on each day.

I’ve made an error. I will correct later.

Nice problem.

 

[The Tall Luthier]

Yes, sometime between 12.37 and 12.38, assuming constant speed on each day.

You are correct and I didn’t ask for a time. It’s one of those problems that requires very little maths but a shift in thinking.

The shift is
.
I
I
I
I
I
I
I
I
I
I
I
I

I
I
You do the journey up and on the same day someone else does the journey down.

Will you cross paths?

Ergo same time, same place.

 

[Amarillo]

You are correct and I didn’t ask for a time. It’s one of those problems that requires very little maths but a shift in thinking.

The shift is
.
I
I
I
I
I
I
I
I
I
I
I
I

I
I
You do the journey up and on the same day someone else does the journey down.

Will you cross paths?

Ergo same time, same place.

I have redone my calculations and now think the time the two Californias pass the same location is between 1.06pm and 1.07pm. More precisely, but not exactly, 13:06:04.7 (4.7 seconds after 1.06pm).

This sort of question was standard fodder for O level maths in the 1960s.

Solution | At what time would these two trains meet? | Introducing Calculus | Underground Mathematics

Section Solution from a resource entitled At what time would these two trains meet?.

undergroundmathematics.org

It is telling how much my maths has deteriorated that it took me two days to get my head around the problem.

 

[The Tall Luthier]

I have redone my calculations and now think the time the two Californias pass the same location is between 1.06pm and 1.07pm. More precisely, but not exactly, 13:06:04.7 (4.7 seconds after 1.06pm).

This sort of question was standard fodder for O level maths in the 1960s.

Solution | At what time would these two trains meet? | Introducing Calculus | Underground Mathematics

Section Solution from a resource entitled At what time would these two trains meet?.

undergroundmathematics.org

It is telling how much my maths has deteriorated that it took me two days to get my head around the problem.

I spent a decade teaching maths and another decade writing the country’s biggest school maths website. I’ve been teasing kids with that kind of thing for too long.

I love that kind of stuff.

 

[Amarillo]

I spent a decade teaching maths and another decade writing the country’s biggest school maths website. I’ve been teasing kids with that kind of thing for too long.

I love that kind of stuff.

Here’s another.

On a standard 30cm / 12inch classroom ruler, at what measurement are cms the same as inches?

How is this different for a 15cm / 6” ruler?

45cm / 18”?

What is the general equation?

 

[yossarian]

Here’s another.

On a standard 30cm / 12inch classroom ruler, at what measurement are cms the same as inches?

Hurricane Electric Mathematics | Questions

math.he.net

Assumes 12" is aligned with 0cm.

 

[Amarillo]

Hurricane Electric Mathematics | Questions

math.he.net

Assumes 12" is aligned with 0cm.

I have a very different answer. And yes, 0cm is aligned with 12” and 30cm with 0”, implying 1” = 2.5cm.

 

[yossarian]

Mmmm was a little hasty: https://math.he.net/question/238f8e70b886ce65a99dc4fba8875b865e5caf17

I used 2.54 and alignment as mentioned.

 

[The Tall Luthier]

Here’s another.

On a standard 30cm / 12inch classroom ruler, at what measurement are cms the same as inches?

How is this different for a 15cm / 6” ruler?

45cm / 18”?

What is the general equation?

Good old y = mx + c

The general for 2.5 cm to the inch is
equilibrium = 5 x width in inches / 7

 

[The Tall Luthier]

Here’s another one!

Plenty of numbers to crunch through if you’re doing it wrong.

A tennis competition takes place with a million and one players. The victor wins a Cali.

How many matches must there be?

If one player can’t be paired, they get a ‘by’ into the next round.

So for clarity, in the first round there will be 500,000 matches and one player who gets to round two without playing.

 

[Amarillo]

Here’s another one!

Plenty of numbers to crunch through if you’re doing it wrong.

A tennis competition takes place with a million and one players. The victor wins a Cali.

How many matches must there be?

If one player can’t be paired, they get a ‘by’ into the next round.

So for clarity, in the first round there will be 500,000 matches and one player who gets to round two without playing.

The way to solve is start with 2 players, then 3, until a pattern is seen for a general solution.

 

[The Tall Luthier]

The way to solve is start with 2 players, then 3, until a pattern is seen for a general solution.

You could, it would work. A better way might be to think about the two things that happen at the end of every match. One person wins and one loses and LEAVES?

 

[Amarillo]

Here’s another one!

Plenty of numbers to crunch through if you’re doing it wrong.

A tennis competition takes place with a million and one players. The victor wins a Cali.

How many matches must there be?

If one player can’t be paired, they get a ‘by’ into the next round.

So for clarity, in the first round there will be 500,000 matches and one player who gets to round two without playing.

I think it is 20 matches because 2^20 = 1,048,576, the power of 2 just above 1,000,001.

 

[The Tall Luthier]

I think it is 20 matches because 2^20 = 1,048,576, the power of 2 just above 1,000,001.

I’m afraid not.
Solution below
I
I
U
U
U
U
U
Uu
Y
U
U
U
Y
Y
Y
Every match someone goes home, they lost. In a competition with 1m +1 players you will need 1m matches to send home 1m players leaving you with a winner.

 

[yossarian]

Sometimes a recursive algorithm is the simplest solution:

Scastie - An interactive playground for Scala.

def matches( players:Int): Int = { players match { case 0 => 0 case 1 => 0 case 2 => 1 case _ => players / 2 + matches ((players +1) / 2) } } matches(1000001)

scastie.scala-lang.org